ピープルアナリティクスの初めの一歩を踏み出すには①
はじめに
弊社ではこれまで多くの企業様のピープルアナリティクス導入を支援して参りましたが、その際にネックとなることが多いのは、企業内のデータです。分析しようするデータが分析に適した形で保存されていないため分析ができない、あるいは分析手法が非常に高度なものとなってしまうことが往々にしてあります。以下に説明したいと思います。
ピープルアナリティクスにおける分析手法とデータの関係
ピープルアナリティクスにおける分析の典型的なパターンは、○○と△△の関係性を分析するというものになります。その際に、どちらかを原因、結果と考えて、原因にあたるものを説明変数、結果にあたるものを目的変数と呼びます。この原因と結果に関しては因果関係が検証されている必要はなく、とりあえず、どちらか原因と考えられるもの、結果と考えられるものを想定するのがポイントです。ここでのポイントとしては説明変数は複数同時に用いることが出来るのに対して、目的変数は原則1つであるという点です。たとえば、従業員の業務成績を目的変数、従業員の採用時の評価と勤続年数を説明変数とすることが考えられます。
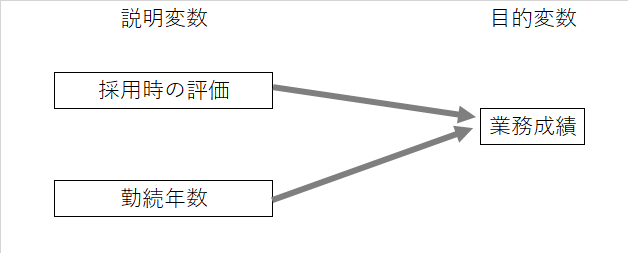
この後には分析手法を選択することになります。その際に目的変数、説明変数として投入するデータの形式によって、分析手法の候補が決まります。一般的には、目的変数のデータの形式によって分析手法がほぼ決まり、目的変数のデータの形式によって分析手法の難易度が決まります。
それでは、データの形式としてはどのようなものがあるでしょうか?大きくは、給与額や勤続年数といった数値として扱えるデータ、あり/なし・Yes/Noのような2つの状態を表すデータ、優/良/可/不可のような3段階以上で序列を表すデータです。
数値として扱えるデータ
まず、数値として扱えるデータです。例としては年齢、残業時間、労働時間、給与・賞与額、0%~100%の目標達成率、勤続年数、試験の点数といったデータです。なお、面接の評価などで、A、B、C、D、Eのような序列を表すデータであっても、後述するように5段階以上で評価間の等間隔性が満たされれば、A=1、B=2,…のように数値を割り当てて数値として扱っても実務上問題ないケースが多いです。
数値として扱えるデータは足し引きが可能なため、平均値、分散といった指標を計算することが出来ます。分析手法も相関係数や回帰分析といった初歩的な手法を適用することが可能です。たとえば試験の点数が0~100点の評価だったとして、面接の評価(10段階評価)との関連を相関係数を算出して検討することが考えられます。
2つの状態を表すデータ
次は、あり/なし・Yes/Noのような2つの状態を表すデータです。このタイプのデータには、「昇進した/しなかった」、「在職中/退職済み」、「勤務中/休職中」、「内定した/内定しなかった」、「内定辞退した/入社した」といったデータが含まれます。
このようなデータは、説明変数の場合は、比較的扱いが簡単です。
たとえば、内定辞退した学生と内定を辞退せず入社した学生で面接時の評価(10段階で評価)が異なるのかを調べたい場合は、それらの2つの群で面接評価の平均に差があるかを調べることが考えられます。この場合、先ほどの回帰分析を適用することも可能ですが、t検定という手法で2群の平均値の差が統計的に意味のある差なのかを検討することも可能です。
一方で、こういった2つの状態を取るデータが目的変数となる場合は難易度が高くなります。たとえば、学生の面接の評価を説明変数として、内定辞退したか入社したかを目的変数としたいとします。この場合、たとえば、ロジスティック回帰分析という若干高度な分析を用いることになります。もちろん、先述したように、目的変数と説明変数を逆転させて、学内定辞退したか入社したかを説明変数、学生の面接の評価を目的変数とすることも考えられますが、面接の評価と筆記試験の点数の2つを説明変数として分析したい場合は、ロジスティック回帰分析を用いる必要があります。
さらに、序列のない3つ以上の状態を分析することも可能ですが、この場合には相当高度な分析手法が必要となります。たとえば、内定を出した学生に関して、面接の評価、性格テストの結果を説明変数として、「自社に入社」、「競合A社に入社」、「その他企業に入社または不明」の3つの状態を目的変数として、面接の評価と性格テストの結果と内定後の学生の行動の関連を分析することも可能ですが、以下の「序列を表すデータ」に用いられるものよりも高度な分析手法が必要となります。
序列を表すデータ
最も扱いが難しいのが人事評価結果のS、A、B、Cのような序列を表すデータです。この場合、たとえば、S=4、A=3、B=2、C=1のように数値を割当てて分析すれば良いと思われるかもしれませんが、注意が必要です。このように数値化することは、SとAの評価の差、AとBの評価の差、BとCの評価の差が等間隔であることを仮定することになります。したがって、Sはよほど例外的な業績を上げた場合にのみ付けるとか、Cは期中で休職した等の場合にしか付けないといった運用がされている場合は、上記のような評価の間の差が等間隔であるという仮定が満たされないことになります。
序列を表すデータであっても説明変数とする場合は比較的簡単です。面接でS、A、B、Cのような評価を付けていた場合、筆記試験の成績(0~100点)との関連を見たいとします。その場合、たとえば、S、A、B、Cの群ごとに、筆記試験の成績の平均を出し、差があるかどうかを調べることが考えられます。やや高度ですが、SとA、SとB、SとCのように2群ずつ見て筆記試験の平均値の差に統計的な意味があるのかを調べる方法もあります。
一方で、序列を表すデータを目的変数として分析したい場合は各段に難しくなります。たとえば、入社1年目の社員の期末の評価(S、A、B、C)を目的変数とし、採用試験の評価(0~10)、配属部署(本社/工場)を説明変数として分析したいとします。その場合、分析は可能ですが、かなり高度な手法を用いる必要が出てきます。統計分析に土地勘のある方であれば分析は可能ですが、その結果を統計分析に土地勘のない上司や経営層が理解するのはかなりハードルが高いと考えられます。
序列があるデータを回避するには?
上記のような序列のあるデータによる困難さを回避する方法としては2つあります。1つは上述したように、序列のあるデータはなるべく説明変数として扱うということです。
もう一つの対処法は、そもそも序列を表すデータを作成する前に、数値として扱えるデータを作成するという方法です。たとえば、人事評価であれば、評価者にはS、A、B、C、Dといった序列としてではなく、1~10の10段階で評価してもらいます。その際に、1と2の間、2と3の間、、、というように数値の間は等間隔であることを想定して評価してもらいます。この方法で10段階評価を評価者に付けてもらい、その後の人事考課につながる最終評価は、10段階評価をもとにS、A、B、Cといった序列のあるデータに変換します。つまり、従業員の評価に関するデータとして、数値として扱えるデータと序列を表すデータが存在することになります。このようにすれば、評価基準は現在のままで、分析上は10段階評価を用いることにより、ピープルアナリティクスでネックになる序列のあるデータの取り扱いの難しさを回避することができます。
たとえば、入社1年目の従業員の期末の評価が1~10の10段階評価でされていた場合には、期末の評価に、採用試験の評価と配属部署がどのように関連しているのかを回帰分析によって検討することが可能になります。この場合、期末評価を目的変数、採用試験の評価、配属部署を説明変数とします。配属部署が本社と工場の2種類であった場合、本社を0、工場を1という数値データとすれば、
入社1年目の従業員の期末の評価(1~10の10段階)=α×採用試験の評価(0~100)+β×配属部署(本社=0/工場=1)+γ
という式で回帰分析を行うことが考えられます。回帰分析の結果、αがプラスで大きい値であれば採用試験の評価が高い従業員ほど1年後の評価も高いという関係がある可能性がありますし、マイナスで大きい場合は、採用試験の評価と1年後の評価が逆転している可能性があります。同様に、βは、採用試験の評価が同じ従業員における配属部署による差(工場と本社の差)を表しますので、βがプラスに大きい場合は、同じ採用試験の評価であれば、工場配属の入社1年目の従業員の方が1年後の評価が高いことを意味します。
以 上
【登録者800人突破!】行動科学・データサイエンス、職場のメンタルヘルス、健康経営等に関する、人事担当者様、産業保健スタッフ・心理職の方に有用な情報を配信する株式会社ベターオプションズによる無料不定期メールマガジンはこちらから登録できます。
※登録後に「申し訳ありませんが、サーバーエラーが発生したようです。また、後ほどお試しください」というメッセージが表示されることがありますが、登録は完了しておりますのでご安心ください。
最新情報を発信する弊社LINE公式アカウントはこちらです!
![]()
